- Unrotated factor solutions extract factors in the order of their variance extracted.
- The first factor tends to be a general factor with almost every variable loading significantly, and it accounts for the largest amount of variance. The second and subsequent factors are then based on the residual amount of variance. Each accounts for successively smaller portions of variance.
- The second and subsequent factors are then based on the residual amount of variance. Each accounts for successively smaller portions of variance.
- The ultimate effect of rotating the factor matrix is to redistribute the variance from earlier factors to later ones to achieve a simpler, theoretically more meaningful factor pattern.
- The simplest case of rotation is an orthogonal factor rotation, in which the axes are maintained at 90 degrees.
- It is also possible to rotate the axes and not retain the 90-degree angle between the reference axes. When not constrained to being orthogonal, the rotational procedure is called an oblique factor rotation.
ORTHOGONAL ROTATION METHODS
- In practice, the objective of all methods of rotation is to simplify the rows and columns of the factor matrix to facilitate interpretation.
- In a factor matrix, columns represent factors, with each row corresponding to a variable’s loading across the factors.
- By simplifying the rows, we mean making as many values in each row as close to zero as possible (i.e., maximizing a variable’s loading on a single factor).
- By simplifying the columns, we mean making as many values in each column as close to zero as possible (i.e., making the number of high loadings as few as possible).
- Three major orthogonal approaches have been developed:
QUARTIMAX
- The ultimate goal of a QUARTIMAX rotation is to simplify the rows of a factor matrix that is, QUARTIMAX focuses on rotating the initial factor so that a variable loads high on one factor and as low as possible on all other factors.
- In these rotations, many variables can load high or near high on the same factor because the technique centers on simplifying the rows
VARIMAX
- In contrast to QUARTIMAX, the VARIMAX criterion centers on simplifying the columns of the factor matrix.
- With the VARIMAX rotational approach, the maximum possible simplification is reached if there are only 1s and 0s in a column. That is, the VARIMAX method maximizes the sum of variances of required loadings of the factor matrix.
- Recall that in QUARTIMAX approaches, many variables can load high or near high on the same factor because the technique centers on simplifying the rows.
- With the VARIMAX rotational approach, some high loadings (i.e., close to –1 or +1) are likely, as are some loadings near 0 in each column of the matrix. The logic is that interpretation is easiest when the variable-factor correlations are (1) close to either +1 or –1, thus indicating a clear positive or negative association between the variable and the factor; or (2) close to 0, indicating a clear lack of association.
- This structure is fundamentally simple. Although the QUARTIMAX solution is analytically simpler than the VARIMAX solution, VARIMAX seems to give a clearer separation of the factors.
- In general, Kaiser’s experiment indicates that the factor pattern obtained by VARIMAX rotation tends to be more invariant than that obtained by the QUARTIMAX method when different subsets of variables are analyzed. The VARIMAX method has proved successful as an analytic approach to obtaining an orthogonal rotation of factors.
EQUIMAX
- Approach is a compromise between the QUARTIMAX and VARIMAX approaches. Rather than concentrating either on simplification of the rows or on simplification of the columns, it tries to accomplish some of each. EQUIMAX has not gained widespread acceptance and is used infrequently.
OBLIQUE ROTATION METHODS
- Oblique rotations are similar to orthogonal rotations, except that oblique rotations allow correlated factors instead of maintaining independence between the rotated factors.
- Where several choices are available among orthogonal approaches, however, most statistical packages typically provide only limited choices for oblique rotations.
- For example, SPSS provides OBLIMIN;
- SAS has PROMAX and ORTHOBLIQUE;
- and BMDP provides DQUART, DOBLIMIN, and ORTHOBLIQUE.
- The objectives of simplification are comparable to the orthogonal methods, with the added feature of correlated factors. With the possibility of correlated factors, the factor researcher must take additional care to validate obliquely rotated factors, because they have an additional way (nonorthogonality) of becoming specific to the sample and not generalizable, particularly with small samples or a low casesto-variable ratio.
SELECTING AMONG ROTATIONAL METHODS
- No specific rules have been developed to guide the researcher in selecting a particular orthogonal or oblique rotational technique.
- In most instances, the researcher simply utilizes the rotational technique provided by the computer program.
- Most programs have the default rotation of VARIMAX, but all the major rotational methods are widely available.
- However, no compelling analytical reason suggests favoring one rotational method over another. The choice of an orthogonal or oblique rotation should be made on the basis of the particular needs of a given research problem.
- Hair, J. F., Black, W. C., Babin, B. J., & Anderson, R. E. (2013). Multivariate data analysis (8th ed.). Boston: Cengage.


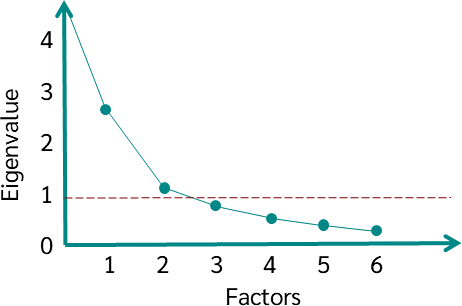






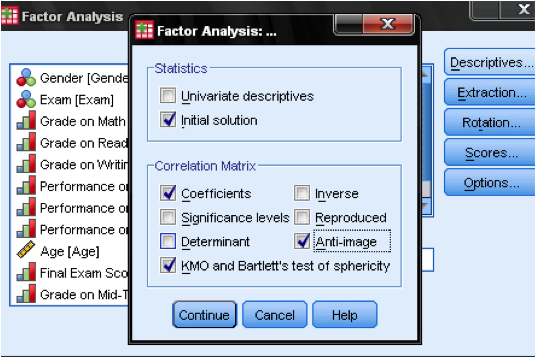












:max_bytes(150000):strip_icc():format(webp)/statistics-ae8f1320de174c279eeeee49c4087917.jpg)