Zeno's paradoxes

Nghịch lý Zeno (Zeno’s paradoxes) là tập hợp các nghịch lý nổi tiếng do triết gia Hy Lạp Zeno xứ Elea (thế kỷ V TCN) nêu ra nhằm phản bác quan niệm về chuyển động liên tục, đặc biệt để bảo vệ quan điểm của sư phụ ông – Parmenides, người cho rằng chuyển động chỉ là ảo ảnh.

Một số nghịch lý nổi bật của Zeno

Trong số khoảng 40 nghịch lý mà Zeno đề xuất, ba nghịch lý sau là nổi tiếng và có ảnh hưởng nhất:

Nghịch lý Achilles và con rùa (Achilles and the Tortoise)

• Lập luận: Trong một cuộc chạy đua, người chạy nhanh nhất (Achilles) sẽ không bao giờ bắt kịp người chạy chậm nhất (Con rùa) nếu con rùa được xuất phát trước.

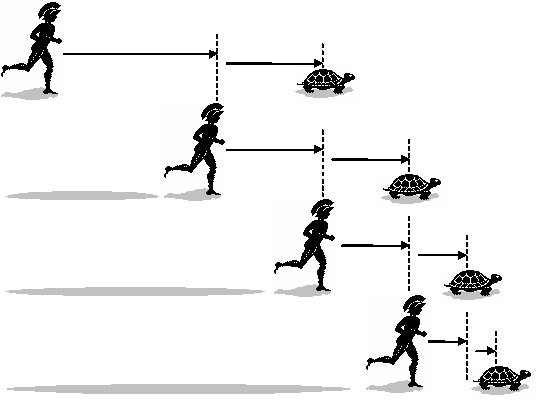
Giải thích của Zeno: Để Achilles bắt kịp con rùa, anh ta phải đến được điểm mà con rùa đã bắt đầu. Khi Achilles đến điểm đó, con rùa đã di chuyển thêm một đoạn ngắn khác. Cứ như vậy, Achilles phải liên tục đến một điểm mới mà con rùa vừa rời đi. Quá trình này tạo ra một chuỗi vô hạn các điểm, và dường như Achilles phải hoàn thành vô số nhiệm vụ (vượt qua vô số khoảng cách nhỏ dần) để bắt kịp con rùa. Do đó, Zeno kết luận rằng việc bắt kịp là không thể.

 

(Nguồn:https://ibmathsresources.com/2018/11/30/zenos-paradox-achilles-and-the-tortoise-2/ )

 Nghịch lý Phân đôi (Dichotomy Paradox)

• Nghịch lý này tập trung vào sự bất khả thi của việc bắt đầu chuyển động.Lập luận: Để đi từ điểm A đến điểm B, bạn phải đi được một nửa quãng đường (1/2 trước. Để đi được 1/2 quãng đường đó, bạn phải đi được một nửa của nó, tức là 1/4 quãng đường trước. Cứ tiếp tục như vậy, trước khi bắt đầu bất kỳ quãng đường nào, bạn phải hoàn thành một nửa của quãng đường đó.

• Kết luận: Vì quá trình chia đôi này diễn ra vô hạn lần, Zeno cho rằng không có điểm bắt đầu thực sự cho chuyển động, do đó không thể di chuyển đến bất cứ đâu.

(Nguồn: https://www.linkedin.com/pulse/xenos-paradoxes-concept-infinity-cem-surmen-cfa-xbvif )

Nghịch lý Mũi tên (Arrow Paradox)

• Nghịch lý này thách thức khái niệm chuyển động trong thời gian.

• Lập luận: Zeno cho rằng, nếu một mũi tên đang bay, tại bất kỳ khoảnh khắc (instant) thời gian nào, mũi tên đó phải chiếm một vị trí cố định bằng với kích thước của nó. 

• Kết luận: Nếu mũi tên đứng yên tại mỗi khoảnh khắc thời gian, và thời gian hoàn toàn bao gồm các khoảnh khắc, thì mũi tên phải đứng yên trong suốt quỹ đạo của nó. Tức là, chuyển động là không tồn tại.

(Nguồn: https://ericgerlach.com/greek-philosophy-zeno/ )

Các nhóm nghịch lý chính

Nghịch lý về số lượng (Paradoxes of Plurality)

• Argument from Denseness: Nếu có nhiều “thực thể”, thì giữa bất kỳ hai thực thể đó luôn có một thực thể khác, dẫn đến vô tận; nhưng nếu vô tận thì không phải “nhiều” theo nghĩa có số lượng xác định, do vậy dẫn đến mâu thuẫn. 

• Argument from Finite Size: Nếu nhiều thực thể tồn tại, mỗi thực thể phải có kích thước; nếu kích thước bằng 0 thì không tồn tại; nếu nhiều phần có kích thước thì tổng sẽ vô hạn, dẫn tới rằng vật thể hữu hạn phải vô hạn. 

• Argument from Complete Divisibility: Nếu vật thể có thể chia mãi và mãi (chia đôi, rồi chia đôi…), thì nó sẽ hoặc không còn kích thước nào (chỉ điểm) hoặc phải vô tận, dẫn đến mâu thuẫn với “vật hữu hạn chuyển động”. 

Nghịch lý về chuyển động (Paradoxes of Motion)

• Dichotomy (Phân đôi): Trước khi chuyển động tới đích, phải đến nửa đường; trước đó phải đến nửa của nửa; và cứ thế vô tận, như vậy sẽ không bao giờ đến đích. Đây là lập về Achilles and the Tortoise (A­chi­lê và rùa), lập luận về mũi tên đã đề cập ở trên. 

Các nghịch lý khác

• Paradox of Place: Mỗi vật có một “nơi” (“place”), nhưng nơi đó lại có “nơi” của nó, và cứ thế vô tận, dẫn đến mâu thuận trong vấn đề về khái niệm “nơi chốn”. 

• Grain of Millet (Hạt kê): Nếu cả bó kê khi rơi thì nghe tiếng, vậy mỗi hạt sẽ nghe tiếng? Zeno lập luận các hạt riêng rẽ sẽ không tạo tiếng dẫn đến mâu thuẫn. 

Giải pháp hiện đại và ý nghĩa toán học

 Vấn đề về các bước vô hạn của Zeno đã được giải quyết một cách chính thức vào thế kỷ 17 với sự phát triển của Vi tích phân (Isaac Newton và Gottfried Wilhelm Leibniz).Các nhà toán học chứng minh rằng việc cộng vô số phần tử nhỏ dần (như trong chuỗi 1/2 + 1/4 +1/8 +...) có thể cho ra một tổng hữu hạn (trong trường hợp này là bằng 1). Điều này có nghĩa là, một khoảng cách hữu hạn vẫn có thể được chia thành vô số phần tử, nhưng tổng thời gian để vượt qua vô số phần tử đó vẫn là một khoảng thời gian hữu hạn. Achilles thực sự bắt kịp con rùa.

Mặc dù đã được giải quyết về mặt toán học, Nghịch lý Zeno vẫn là một tài liệu tham khảo quan trọng trong triết học, vật lý và toán học, làm nổi bật xung đột giữa trực giác và logic nghiêm ngặt, đồng thời thúc đẩy các cuộc thảo luận sâu sắc về bản chất của không gian, thời gian và vô hạn. Thậm chí, nó còn có ảnh hưởng đến khái niệm hiện đại như Hiệu ứng Zeno lượng tử (Quantum Zeno effect) trong cơ học lượng tử.

Nguồn tham khảo

• https://blogm4e.wordpress.com/2017/07/21/nghich-ly-zeno-cau-chuyen-cua-achilles-va-con-rua/
• https://tiasang.com.vn/doi-moi-sang-tao/vat-ly-luong-tu-tai-goi-mo-nghich-ly-zeno/
• https://plato.stanford.edu/entries/paradox-zeno/
• https://ibmathsresources.com/2018/11/30/zenos-paradox-achilles-and-the-tortoise-2/