Outliers in Regression

 Trong hồi quy có thể kể đến 3 dạng quan sát bất thường:

• Regression Outliers
• Leverage 
• Influential Observations

Regression Outliers

Quan sát ngoại lệ trong hồi quy là một quan sát có giá trị bất thường của biến phụ thuộc Y khi sánh với các trường hợp khác có cùng giá trị của các biến độc lập X

(Nguồn: https://static.wixstatic.com/media/9a9006_296dff8aa18840bebbd563ef81eee666~mv2.gif)

 

Leverage 

• Các giá trị bất thường khi xem xét chỉ với các biến độc lập thì được gọi là điểm đòn bẩy. Một quan sát có giá trị X bất thường - tức là nó khác xa với giá trị trung bình của X - tức là có khả năng tiềm ẩn làm ảnh hưởng đến kết quả hồi quy. Tuy nhiên, giá trị đòn bẩy của một quan sát cao thì không nhất thiết có nghĩa là quan sát đó có ảnh hưởng đến hệ số hồi quy.

(Nguồn: https://www.researchgate.net/publication/265097085_Do_theme_parks_deserve_their_success)

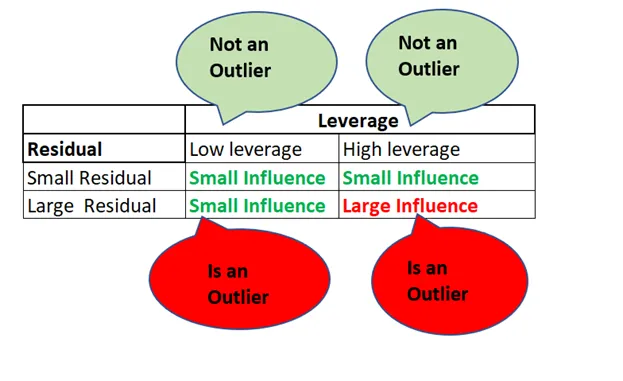
Influential Observations

Những quan sát có giá trị đòn bẩy cao và thực sự có ảnh hưởng đến hệ số góc của các biến độc lập trong kết quả hồi quy thì được gọi là điểm ảnh hưởng (Influential observations). Nghĩa là, chỉ khi một quan sát có đòn bẩy cao và là một ngoại lệ về mặt giá trị xét theo biến phụ thuộc Y thì nó mới ảnh hưởng mạnh mẽ đến đường hồi quy. Nói cách khác, một influential observation  phải có giá trị Xbất thường với giá trị Y bất thường tương ứng với giá trịX của nó. Trong những trường hợp như vậy, cả hệ số chặn và hệ số góc đều bị ảnh hưởng khi sử dụng quan sát này trong dữ liệu.

 

(Nguồn: https://pub.towardsai.net/the-outlier-story-leverage-and-influential-point-in-linear-regression-31517f2ca203)

Nguồn tham khảo:

•  https://ouzhang.me/blog/outlier-series/outliers-part3/
• https://pub.towardsai.net/the-outlier-story-leverage-and-influential-point-in-linear-regression-31517f2ca203
• https://www.solutions4statistics.com/post/2017/07/27/detect-remove-outliers-in-regression