Finding Outliers in a univariated way

 Một univariate outlier là một điểm dữ liệu bất thường, khác biệt so với các quan sát khi xem xét trên một biến cụ thể.

Có thể có nhiều phương pháp khác nhau để phát hiện một  univariate outlier 

Phương pháp 1:  Sắp xếp bảng dữ liệu (sorting data)

Sắp xếp biểu dữ liệu là một cách đơn giản nhưng hiệu quả để phát hiện các giá trị bất thường. Các giá trị bất thường thường xảy ra ở những quan sát ứng với giá trị nhỏ nhất hoặc lớn nhất sau khi sắp xếp.

Phương pháp 2: Vẽ đồ thị dữ liệu 

Biểu đồ hình hộp, biểu đồ histogram và biểu đồ phân tán có thể làm nổi bật các giá trị ngoại lệ.

 

Phương pháp 3: Sử dụng  Z - Score 

Z-score có thể định lượng mức độ bất thường của một quan sát khi dữ liệu ctuân theo phân phối chuẩn. Để tính điểm Z cho một quan sát, thì ta lấy giá trị của quan sát đó, trừ giá trị trung bình và chia cho độ lệch chuẩn. Về mặt toán học, công thức cho quá trình đó như sau: 

\begin{equation} Z=\frac{X-\mu}{\sigma}\end{equation}

Điểm Z của một quan sát càng xa 0 thì nó càng bất thường. Giá trị giới hạn tiêu chuẩn để tìm các giá trị ngoại lệ là điểm Z bằng +/- 3 hoặc cao. Tuy nhiên, nếu dữ liệu của bạn không tuân theo phân phối chuẩn thì phương pháp này có thể không chính xác.

Lưu ý rằng điểm Z có thể gây hiểu nhầm với các tập dữ liệu nhỏ vì điểm Z tối đa bị giới hạn ở 

\begin{equation}  \(\frac{n-1}{\sqrt{n}}\). \end{equation}

(Nguồn: https://www.almabetter.com/bytes/articles/outlier-detection-methods-and-techniques-in-machine-learning-with-examples)

 

Ngoài ra, hãy lưu ý rằng sự hiện diện của điểm ngoại lệ sẽ làm mất đi điểm Z vì nó làm tăng giá trị trung bình và độ lệch chuẩn như chúng ta đã thấy trước đó. Lưu ý rằng tất cả các điểm Z đều âm ngoại trừ v của ngoại lệ

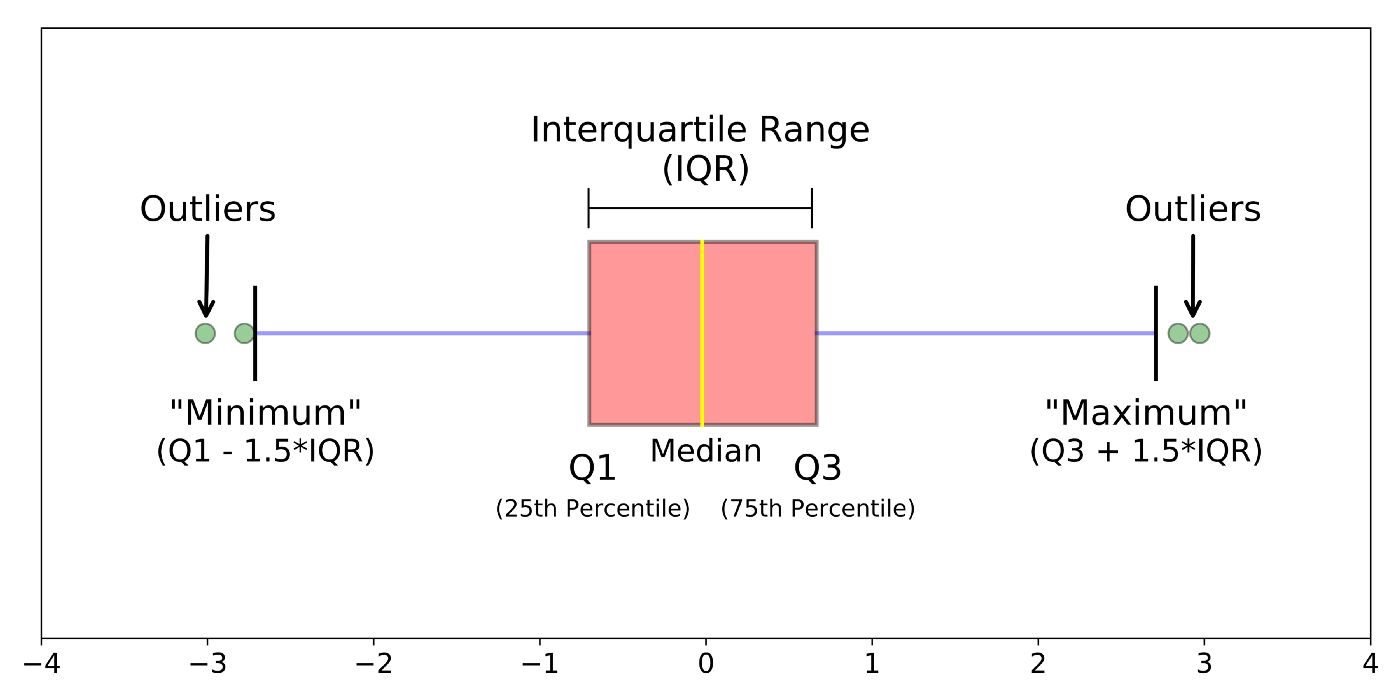
Phương pháp 4: Sử dụng khoảng tứ phân vị (Interquartile Range (IRQ))

Khoảng tứ phân vị (IQR)  có thể giúp xác định outliers vì nó vạch ra ranh giới giá trị để nhận biết những con số bất thường. IQR là 50% ở giữa của tập dữ liệu. Đó là phạm vi giá trị giữa tứ phân vị thứ ba và tứ phân vị thứ nhất (Q3 – Q1).

Chúng ta có thể lấy các giá trị IQR, Q1 và Q3 để tính toán các hàng rào ngoại lệ sau cho tập dữ liệu của mình: bên ngoài bên dưới, bên trong bên dưới, bên trong bên trên và bên ngoài bên trên. Những hàng rào này xác định xem các điểm dữ liệu có phải là ngoại lệ hay không và chúng ở mức độ nhẹ hay mức độ ngoại lệ cực đoan. Các giá trị nằm bên trong hai hàng rào bên trong không phải là giá trị ngoại lệ.

 

(Nguồn: https://raw.githubusercontent.com/NaysanSaran/stats101)  

Để tính toán hàng rào ngoại lệ, hãy làm như sau:

• Tính toán IQR cho tập dữ liệu và nhân nó với 1,5 và 3. Chúng tôi sẽ sử dụng các giá trị này để tính hàng rào bên trong và bên ngoài.

• Tính toán hàng rào bên trái:  Lấy giá trị Q1 và trừ hai giá trị ở bước 1, thu được hàng rào trong và ngoài cho những quan sát thấp bất thường. 

• Tính toán hàng rào bên phải. Lấy giá trị Q3 và cộng hai giá trị từ bước 1, thu được hàng rào trong và ngoài cho những quan sát cao bất thường n.   

Phương pháp IQR rất hữu ích vì nó sử dụng phân vị phần trăm, không phụ thuộc vào phân bổ cụ thể. Ngoài ra, phần trăm tương đối chắc chắn đối với sự hiện diện của các giá trị ngoại lệ so với các phương pháp định lượng khác.

Phương pháp 5:  Sử dụng bách phân vị (Percentiles)

Với phương pháp bách phân vị, tất cả các quan sát nằm ngoài khoảng được hình thành bởi phân vị 0.025 và 0.975 sẽ được coi là các giá trị ngoại lệ tiềm năng. Các phân vị khác như 0.01 và 0.99; hoặc 0.05 và 0.95 cũng có thể được xem xét để xây dựng khoảng xác định outliers.

Phương pháp 6:  Bộ lọc Hampel (Hampel filter)

Khối Bộ lọc Hampel phát hiện và loại bỏ các ngoại lệ của dữ liệu bằng cách sử dụng mã định danh Hampel. Mã định danh Hampel là một biến thể của quy tắc thống kê ba sigma, được thực hiện bằng cách tính toán trung vị của một khung cửa sổ bao gồm quan sát hiện tại và [(m−1)/2 ] quan sát liền kề, trong đó m là chiều dài khung cửa sổ mà bạn chọn. Sau đó, tính toán độ lệch chuẩn của từng quan sát trong cửa sổ dữ liệu được xem xét. Nếu một quan sát khác với giá trị trung bình nhiều hơn 3 (hoặc một ngưỡng nào đó) nhân với độ lệch chuẩn, thì bộ lọc Hampel sẽ thay thế mẫu bằng giá trị trung vị của cửa sổ đó. 

(Nguồn: https://www.mathworks.com/help/examples/signal/)

 

Phương pháp 7: Dựa vào các kiểm định giả thuyết thống kê

Có ba kiểm định phổ biến:

•  Grubbs’s test: cho phép phát hiện xem giá trị cao nhất hay thấp nhất trong tập dữ liệu có phải là giá trị ngoại lệ hay không.

• Dixon’s test: tương tự như thử nghiệm Grubbs, thử nghiệm Dixon được sử dụng để kiểm tra xem một giá trị thấp hay cao có phải là giá trị ngoại lệ hay không. Vì vậy, nếu có nhiều hơn một ngoại lệ bị nghi ngờ, việc kiểm tra phải được thực hiện riêng lẻ trên các ngoại lệ bị nghi ngờ này.

• Rosner’s test: sử dụng để phát hiện nhiều ngoại lệ cùng một lúc (không giống như thử nghiệm Grubbs và Dixon phải được thực hiện lặp đi lặp lại để sàng lọc nhiều ngoại lệ)

Nguồn: 

• https://ouzhang.me/blog/outlier-series/outliers-part2/
• https://www.introspective-mode.org/univariate-outliers/