What are Assessments?
- Assessments are often mistaken with standardized tests that determine grades and ranks. In reality, assessment is an umbrella term that incorporates standardized tests and many other forms of evaluation. It refers to a wide range of methods that educators use to assess learners at different levels of learning.
- In other words, assessment refers to the systematic gathering of information that evaluates, measures, and documents the performance of learners to give a clear picture of their academic readiness, learning progress, and acquisition of skills. Moreover, assessments help identify the strengths and weaknesses of the students. This helps teachers modify their teaching techniques according to the students’ learning requirements.
- Other than providing diagnostic feedback, assessments motivate students as well as teachers in different ways. Students get a chance to demonstrate their skills and improve through self-assessment, and teachers get directions to help the students perform better in learning through improved instructions.
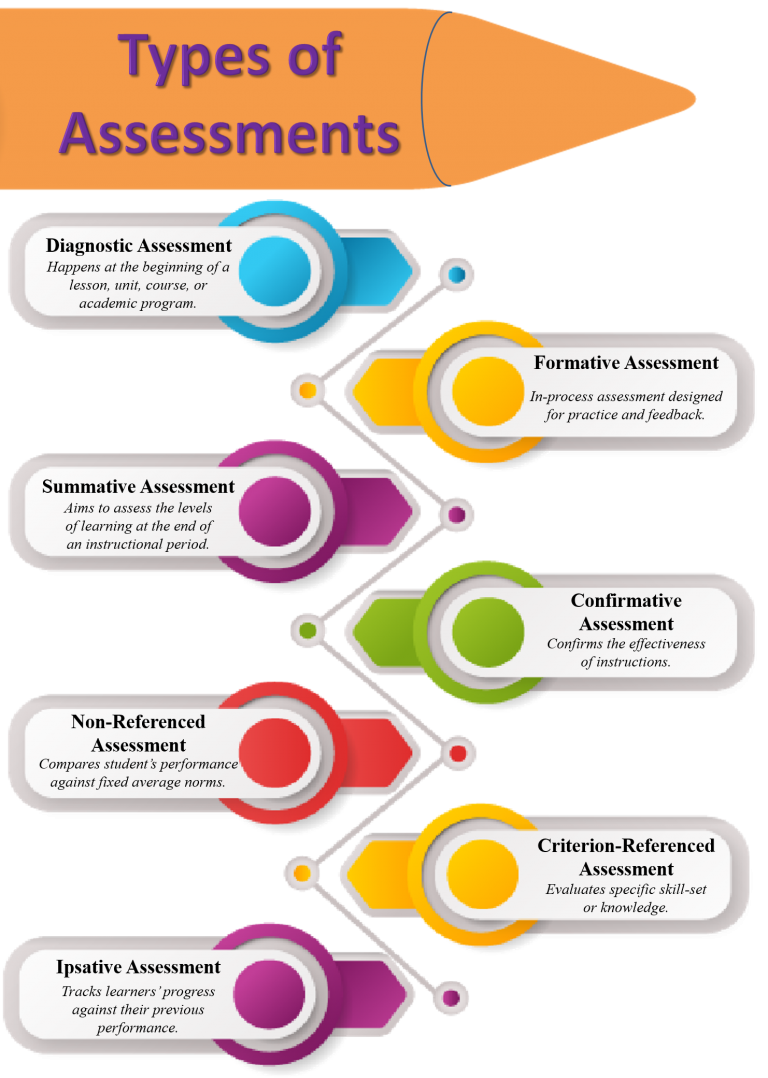
Types of Assessments
1. Diagnostic Assessment or Pre-Assessment
Diagnostic or pre-assessments happen before the beginning of a lesson, unit, course, or any academic program. They are useful for collecting information about the strengths, weaknesses, skills, and knowledge the learners possess. Instructions are designed thereafter as per the learners’ requirements.
2. Formative Assessment
These are the in-process assessments that support learning. A teacher administers formative assessment multiple times during a unit, lesson, or course. They are particularly designed for practice. Additionally, the most important function of formative assessment is to monitor learning and provide feedback to modify instructions.
It acts as a form of continuous learning, covering small content areas while also monitoring the learning process. However, such types of evaluations do not assign ranks and grades.
3. Summative Assessment
This type of assessment aims to assess the learning levels at the end of an instructional period. It attempts to measure the effectiveness of learning, the student’s proficiency, and their success. For this, this method uses tests, assignments, and projects for specific grading and ranking of students.
Moreover, it measures the knowledge, skills, and attitude of the learners in the long run. Hence, it gives an insight into the students’ performance as well as the effectiveness of a teacher’s instructions.
4. Confirmative Assessment
As the name suggests, confirmative assessment is a way to confirm the effectiveness of instructions a year after the end of an instructional period. The ultimate goal here is to check whether the employed instructional strategies are still successful and that the teaching is accurate. Therefore, they are, most importantly, an extensive form of summative assessment.
5. Norm-Referenced Assessment
In this assessment, teachers compare a student’s performance against certain fixed average national norms. For instance, the average grade in English state-wise.
Moreover, it compares the students’ performance with their peers in a competitive environment. Here, the average grade comparison is with the entire school. Hence, this assessment is also referred to as Group/Demographic Assessment.
6. Criterion-Referenced Assessment
Criterion-referenced tests evaluate specific skill-set or knowledge against pre-determined criteria of learning. It checks the learning requirements and abilities of the students at a particular learning stage. These tests evaluate the students on specific goals, objectives, or standards. In other words, it evaluates the entire course curriculum.
7. Ipsative Assessment
Ipsative assessment tests track the learners’ progress against their previous performance. The learners attempt to improve through comparison with previous results.
Nguồn tham khảo:
- https://www.evelynlearning.com/what-are-assessments/